Correct Box Sphere Intersection
02/04/2013
Edit [31/03/2019]: The code presented here (embarrassingly given the name of this article I know) before an edit in 2019 actually contained an error and produced false positives in some cases where the sphere could be closely nestled against the box but not completely intersecting - in this case it would say an intersection was taking place when it was actually not. The code you see here has since been updated to fix this error. I guess the lesson is don't trust code you find on the internet, in particular if it has been written by me!
Testing for intersection between a box and sphere is not as trivial as it may first seem.
I found many resources on the web explaining how to do it, but after struggling for a while I realized all of them listed an incorrect algorithm. What they stated was that you had to try for intersection against all face planes of the box. Some did mentioned briefly that this is flawed, but most didn't seem to even be aware. With a little bit of thought the reason this is incorrect becomes obvious.
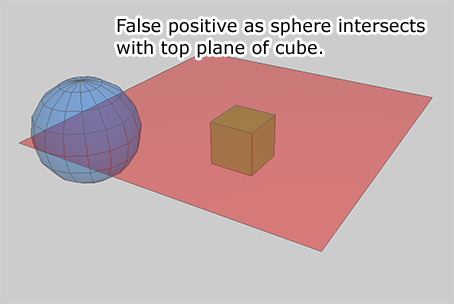
If you simply check for intersection with the face planes of the box you get a bunch of false positives where the planes extend past the ends of the box. While perhaps a few false positives may not be a big deal in some cases, when there are large spheres and acceleration structures such as quad trees, false positives can mean many, many more operations than usual. Actually doing the correct checks are not much more expensive and overall improve performance.
To start we need to write three tests for checking if a sphere is inside, outside or intersecting a plane. This can be done by taking the signed distance from the plane and comparing to the sphere radius.
If the distance is negative and greater than the radius we know it is inside. If the distance is positive and greater than the radius we know it is outside. Finally if the absolute distance is less than or equal to the radius we know there is an intersection.
float plane_distance(plane p, vec3 point) {
return vec3_dot(vec3_sub(point, p.position), p.direction);
}
bool sphere_inside_plane(sphere s, plane p) {
return -plane_distance(p, s.center) > s.radius;
}
bool sphere_outside_plane(sphere s, plane p) {
return plane_distance(p, s.center) > s.radius;
}
bool sphere_intersects_plane(sphere s, plane p) {
return fabs(plane_distance(p, s.center)) <= s.radius;
}
Using these we can test for if a sphere is inside, outside or intersecting a box (specified as 6 planes). The reasoning behind this representation of 6 planes is that we can use it with non axis-aligned boxes, and boxes of odd shapes such as view frustums (which was my original application). When constructing these planes it is important to ensure all the plane normals face outward.
The test for if a sphere is inside a box is easy. Just check that the sphere is inside all of the face planes.
bool sphere_inside_box(sphere s, box b) {
if (!sphere_inside_plane(s, b.front)) { return false; }
if (!sphere_inside_plane(s, b.back)) { return false; }
if (!sphere_inside_plane(s, b.top)) { return false; }
if (!sphere_inside_plane(s, b.bottom)) { return false; }
if (!sphere_inside_plane(s, b.left)) { return false; }
if (!sphere_inside_plane(s, b.right)) { return false; }
return true;
}
The intersection test, our original goal, is a little harder, and for this we will need to know not just if a sphere is inside a plane, but also the closest point on the place where the sphere is intersecting, and also the radius of the circle which is produced by the intersection.
bool sphere_intersects_plane_point(sphere s, plane p, vec3* point, float* radius) {
float d = plane_distance(p, s.center);
vec3 proj = vec3_mul(p.direction, d);
*point = vec3_sub(s.center, proj);
*radius = sqrtf(max(s.radius * s.radius - d * d, 0));
return fabs(d) <= s.radius;
}
Then what we need to do is this: for each face check if there is an intersection, and if there is an intersection then ensure that the distance between the closest point on the intersecting plane is within the radius of the circle of intersection.
bool sphere_intersects_box(sphere s, box b) {
vec3 point;
float radius;
if (sphere_intersects_plane_point(s, b.top, &point, &radius)) {
if (plane_distance(b.left, point) <= radius &&
plane_distance(b.right, point) <= radius &&
plane_distance(b.front, point) <= radius &&
plane_distance(b.back, point) <= radius) {
return true;
}
}
if (sphere_intersects_plane_point(s, b.bottom, &point, &radius)) {
if (plane_distance(b.left, point) <= radius &&
plane_distance(b.right, point) <= radius &&
plane_distance(b.front, point) <= radius &&
plane_distance(b.back, point) <= radius) {
return true;
}
}
if (sphere_intersects_plane_point(s, b.left, &point, &radius)) {
if (plane_distance(b.top, point) <= radius &&
plane_distance(b.bottom, point) <= radius &&
plane_distance(b.front, point) <= radius &&
plane_distance(b.back, point) <= radius) {
return true;
}
}
if (sphere_intersects_plane_point(s, b.right, &point, &radius)) {
if (plane_distance(b.top, point) <= radius &&
plane_distance(b.bottom, point) <= radius &&
plane_distance(b.front, point) <= radius &&
plane_distance(b.back, point) <= radius) {
return true;
}
}
if (sphere_intersects_plane_point(s, b.front, &point, &radius)) {
if (plane_distance(b.top, point) <= radius &&
plane_distance(b.bottom, point) <= radius &&
plane_distance(b.left, point) <= radius &&
plane_distance(b.right, point) <= radius) {
return true;
}
}
if (sphere_intersects_plane_point(s, b.back, &point, &radius)) {
if (plane_distance(b.top, point) <= radius &&
plane_distance(b.bottom, point) <= radius &&
plane_distance(b.left, point) <= radius &&
plane_distance(b.right, point) <= radius) {
return true;
}
}
return false;
}
Once we have these tests, checking if a box is outside is as simple as ensuring it is not inside or intersecting.
bool sphere_outside_box(sphere s, box b) {
return !(sphere_inside_box(s, b) || sphere_intersects_box(s, b));
}
It may seem more expensive but really it is only a handful more dot products and conditionals which the compiler can hopefully optimize away nicely. I feel like capturing the logic and making it clear is more important. Hope this helps any of you who were in my situation!