Local Minima, Saddle Points, and Plateaus
02/10/2018
Various algorithms, such as those used for reinforcement learning or function minimization often present a trade off between exploitation and exploration. The basic idea being that when you are trying to accomplish a task, you have roughly two types of actions you could perform - actions which are good because you know they will bring about a good result, and those which are good because they will give you more information about the task you are trying to achieve.
Imagine that you are at one of your favorite restaurants and trying to decide what to order. One option is to order your favorite dish - the same thing you always order. This option is good because you are pretty certain you will get something you like - we call this exploitation because you are exploiting your previous knowledge about the menu to get a good result. Another option would be to order something new from the menu you've not had before. In the best case you might end up with something even better than your current favorite, but you could also end up with something worse. If you do end up with something worse, although it might seem like a waste, there is still some benefit to having tried something new because at least now you know. You know that you were never missing out on anything and that your existing favorite is even more likely to be the best choice on the menu.
When making a series of decisions there is always a trade-off between the two policies. Being too exploitative means you may pass by good opportunities in favor of sub-optical decisions you already know the result of, while being too exploratory means that you may pass by good opportunities you know in favor of other decisions with results you are less certain will be beneficial!
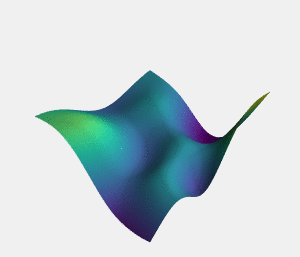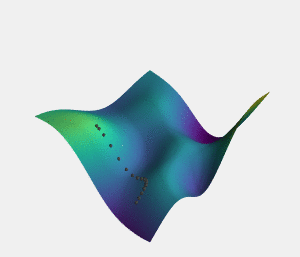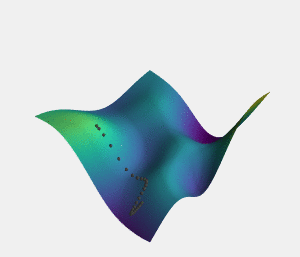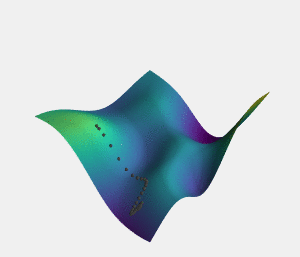
In function minimization (the task of finding the input to a mathematical function which produces the smallest output), the symptom of being too exploitative is getting stuck in a so called "local minima" where an early non-optimal result leads you down a path of no return from which you can't improve. The symptom of being too exploratory on the other hand is a "slow convergence rate", where it takes a long time to find the solution because so much time is spent exploring bad options with just a small chance of improvement on the current best result.
Philosophers, Mathematicians, and Economists have often thought about how this same trade-off is reflected in people's real-life decision making processes. We can view "exploratory" people as those who iterate slowly on task, trying to gain a deep and intimate understanding of a subject by following all references and sub-references. They are people who are easily distracted, and in the finishing stages of a project have difficultly in making those final steps required to get right to the end. On the opposite side of things we see "exploitative" people as being much more goal driven and often capable of achieving their objectives quickly, but with a tendency to iterate towards the first solution which fits - a behavior that can often create unforeseen disadvantages later on down the line.
I think everyone can agree that adaptivity is important - that when you are certain an action will be good it makes sense to take it, while when options seem less likely to produce good outputs it is better to explore - but other than that what is the best general strategy to balance this trade-off? Mathematically, this is a well explored field with many academics working on thought experiments such as the Multi-Armed Bandit problem which present a very pure form of this puzzle, yet even so there is no general consensus.
And although obviously there will always be some balance required between exploitation and exploration, there is actually an interesting and (in some ways profound) argument which often gets overlooked when considering this question more philosophically.
According to this argument (explained below), in situations where there are lots of different potential actions, such as in many real world tasks, a more exploitative policy is almost always a better choice than an exploratory policy. To understand why we need to first take a look at a recent theory on the subject of how "saddle points" manifest themselves in high dimensional spaces.

In the mathematical problem of function minimization saddle points are the name we give to points on the "minimization landscape" which are local minima on one axis but not on others. Intuitively, if we consider function minimization to be similar to the idea of completing a task in the real world, you can think of saddle points as points where taking one particular type of action can no longer improve the result of the task, but where other types of actions can still lead to an improvement. Saddle points are not like local minima in that they are not "dead ends", and "exploitative" methods can still be effective when you encounter them - as long as you are flexible enough to stop moving on the axis which has hit a minima and to start moving on the axis upon which there is still room for improvement.
Then, the theory itself states this: that in very high dimensional spaces (such as those we would use to represent tasks which contain a large number of choices) saddle points are exponentially more likely to occur than local minima. More specifically, the probability of a local minima occurring increases only as you get closer to the real global minima.
One way to think about it a bit more intuitively is something like this: if you are performing a task which has a huge number of potential actions to choose from, it is extremely unlikely that you will encounter a situation where you truly cannot improve because to be in this situation would mean that any action you could take would result in a worse situation than the current one you are in. Yet, as the number of potential actions you can make increases, assuming each action is independent and unique, this situation becomes less and less likely by pure chance alone. If you truly do find that none of your actions can result in an improvement this is probably an indication that you are near the true optical result, because this is the only case in which this kind of situation becomes probable.
So why does this theory have an implication on the philosophical debate on the balance between "exploratory" and "exploitative" behavior? Well, it does, because the most common reason for more exploratory policies is to avoid local minima - to avoid rushing or botching together a solution which may trap you in a difficult situation which you are later unable to escape from. But if local minima are very unlikely to occur in the first place, it entails that this exploratory behavior may be less effective than first thought.
In addition to this, since exploratory policies often do everything they can to avoid local minima, people who employ them may have gained a warped view of the real occurrence rate of these minima - in reality many of the local minima that exploratory policies "avoided" could have been saddle points in disguise. That is - many of the rushed and botched together solutions that the policy was desperately trying to avoid might have actually had subtle hidden fixes or get-out clauses which would have only become apparent after reaching them.
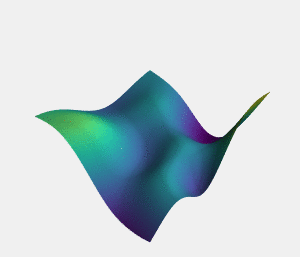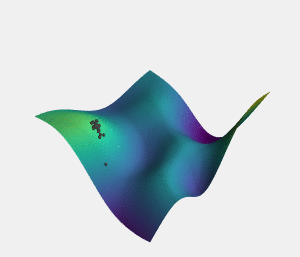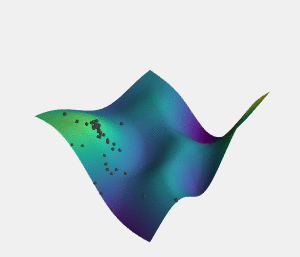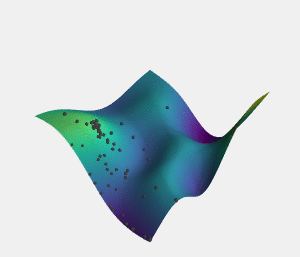
As well as the overly cautious behavior of exploratory policies when it comes to local minima in high dimensional spaces, there is another danger that can badly affect even adaptive policies (policies which attempt to switch between more exploratory behavior and more exploitative behavior based on the curvature of the cost landscape). This danger is plateaus - parts of the optimization landscape where the gradient is very small, or slightly undulating and noisy.
In the real world we can think of plateaus as being akin to situations where it seems that whatever action is taken there is very little change in the result, with an apparent noisy or random component to all the observations.
The danger of plateaus is that the small and noisy gradient tends to encourage adaptive policies to slow down, and begin to explore more, to see if they can find a more optimal path, or at least gather some information about exactly what the effects of their actions are. In may ways this makes sense, as plateaus can resemble local minima in many respects, and the sensible behavior to being caught in a local minima is to start being more exploratory.
But, perhaps counter intuitively, the best way to escape a plateau is to speed up, and to move as fast as possible across the plateau in the rough direction you think it is sloping until you are able to find some curved surface which can give you actual information about which actions might be best.
Again this seems to indicate that in many ways a more exploitative policy may perform better than first expected in high dimensional spaces.
Now, as with all attempts to apply hand wavy mathematical analysis to the real world it is important to take this analysis with a large grain of salt, and to also remember that this only applies in situations where there are many choices or unknowns involved. It doesn't, for example, make sense to apply it to our above restaurant menu example because there are a relatively small number of choices - in this case a basic strategy such as ruling out the items on the menu which you will obviously dislike and then trying the rest exhaustively makes a lot more sense than just picking one item and sticking to it.
But, there is definitely something to be said for having a kind of confidence, focus, and boldness to taking large steps in life, steps that may be risky or short term, but that you believe will take you towards your goal fast. If anything, there is comfort to be had in the idea that perhaps we do not need to be as fearful as we all are of local minima, and that given enough complexity, in any situation there is always a way out. If we believe this mathematical theory applies to real life, maybe it would also tell us to remain focused and move fast toward our goals. To follow our guts until it is shown they are unreliable. To accelerate rather than slow down when progress seems slow and unreliable. To always look for directions which may give better returns than the current one. To be wary of planning ahead for situations we are unsure of. And, to remember that being in a local minima can actually be a good thing - it can indicate we are close to the true optimal solution.
Overall I like to think of the theory of saddle points in high dimensions being a bit like the old adage "as one door closes, another door opens" - it is the idea that while it is certainly possible to reach dead ends in life, there are always opportunities if we look down new paths.