Simple Two Joint IK
18/01/2017
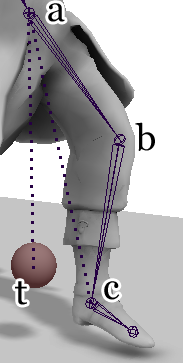
Most animation programmers know that in the case of two joints there exists an analytical solution to the inverse kinematics problem. In short, there is an equation which can give you the required joint angles if you plug in all of the different details of the joints and where you want the end effector to be. But look up exactly what this equation is online and you might be faced with equations that look like this.
This isn't the only way. Two joint IK can be extremely simple and intuitive. Here is a method I think is the easiest to understand and use:
Given the configuration of joints shown to the right, where a is the hip joint,
b is the knee joint, c is the heel joint, and t is the target location
for the heel, we can solve the IK problem with two simple steps.
The first step is to rotate the joints in the chain such that
length of the vector from a to c matches the length of the vector from
a to t. This will allow us to perform the second step of simply rotating the hip around until the heel slides into place.
Step 1: Extend/Contract the Joint Chain
Lets start by getting the lengths of the various vectors involved.
float eps = 0.01;
float lab = length(b - a);
float lcb = length(b - c);
float lat = clamp(length(t - a), eps, lab + lcb - eps);
Here we clamp the length between the hip and the target to the
maximum extension of the two joints (which equals the sum of the lengths of the
joint segments). We can also use some small value eps to limit this extension
to some minimum and maximum amount so the leg never appears full extended or
fully contracted.
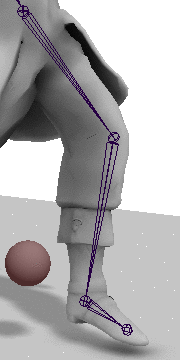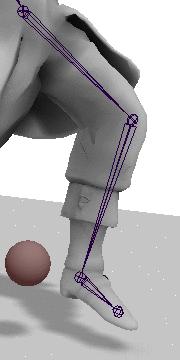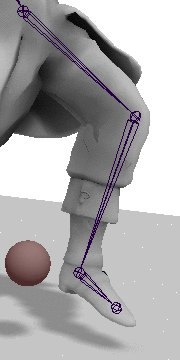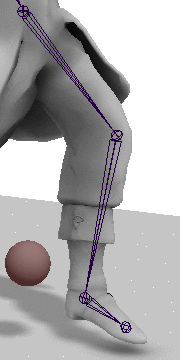
Next we get the current interior angles of the hip and knee joints. For this we can just use the dot product method:
float ac_ab_0 = acos(clamp(dot(
normalize(c - a),
normalize(b - a)), -1, 1));
float ba_bc_0 = acos(clamp(dot(
normalize(a - b),
normalize(c - b)), -1, 1));
We clamp the output of the dot product in the range -1 to 1 before passing it to acos - this removes the occasional numerical errors caused by floating point arithmetic
if the value goes out of the range 1 to -1.
We can now use The cosine rule to get the desired interior angles of these joints which produces a vector from the hip to the heel with the same length as the vector between the hip and the target.
float ac_ab_1 = acos(clamp((lcb*lcb-lab*lab-lat*lat) / (-2*lab*lat), -1, 1));
float ba_bc_1 = acos(clamp((lat*lat-lab*lab-lcb*lcb) / (-2*lab*lcb), -1, 1));
With the current angles and the desired angles, the final angles by which we have to rotate the hip and knee joints are just the
difference between these two values, while the rotation axis is just the cross
product between the vectors from the hip to the knee and the hip to the heel. Since we are working in the world space we have to first
transform this axis into the local space of each joint (since the rotations will be applied locally) with the inverse of the global rotations of the hip a_gr and of the knee b_gr.
vec3 axis0 = normalize(cross(c - a, b - a));
quat r0 = quat_angle_axis(ac_ab_1 - ac_ab_0, quat_mul(quat_inv(a_gr), axis0)));
quat r1 = quat_angle_axis(ba_bc_1 - ba_bc_0, quat_mul(quat_inv(b_gr), axis0)));
Multiply this rotation to the right of the hip joint's local rotation a_lr, as well as the knee joint's local rotation b_lr, and the chain should
now be correctly extended/contracted as shown in the gif above.
a_lr = quat_mul(a_lr, r0);
b_lr = quat_mul(b_lr, r1);
Step 2: Rotate the Heel into place
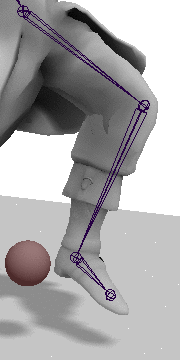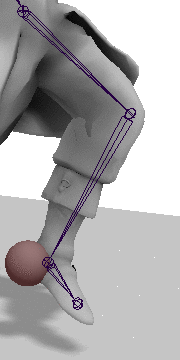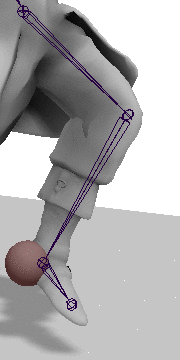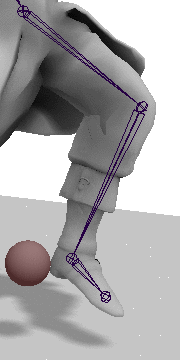
Now there is just one more rotation left. We must rotate the heel into place by rotating on the axis found by taking the cross product of the vector between the hip and heel, and the hip and target, with the angle found by taking the dot product between these two vectors. As before the axis must be transformed into the hip's local space.
float ac_at_0 = acos(clamp(dot(
normalize(c - a),
normalize(t - a)), -1, 1));
vec3 axis1 = normalize(cross(c - a, t - a));
quat r2 = quat_angle_axis(ac_at_0,
quat_mul(quat_inv(a_gr), axis1)));
Just multiply this rotation on the right of the hip joint's local rotation and you're done!
a_lr = quat_mul(a_lr, r2);
Run your forward kinematics again and the heel joint should now be at the target location. That's all - a relatively mathematics free two joint IK. Full code is listed below.
void two_joint_ik(
vec3 a, vec3 b, vec3 c, vec3 t, float eps,
quat a_gr, quat b_gr,
quat &a_lr, quat &b_lr) {
float lab = length(b - a);
float lcb = length(b - c);
float lat = clamp(length(t - a), eps, lab + lcb - eps);
float ac_ab_0 = acos(clamp(dot(normalize(c - a), normalize(b - a)), -1, 1));
float ba_bc_0 = acos(clamp(dot(normalize(a - b), normalize(c - b)), -1, 1));
float ac_at_0 = acos(clamp(dot(normalize(c - a), normalize(t - a)), -1, 1));
float ac_ab_1 = acos(clamp((lcb*lcb-lab*lab-lat*lat) / (-2*lab*lat), -1, 1));
float ba_bc_1 = acos(clamp((lat*lat-lab*lab-lcb*lcb) / (-2*lab*lcb), -1, 1));
vec3 axis0 = normalize(cross(c - a, b - a));
vec3 axis1 = normalize(cross(c - a, t - a));
quat r0 = quat_angle_axis(ac_ab_1 - ac_ab_0, quat_mul(quat_inv(a_gr), axis0));
quat r1 = quat_angle_axis(ba_bc_1 - ba_bc_0, quat_mul(quat_inv(b_gr), axis0));
quat r2 = quat_angle_axis(ac_at_0, quat_mul(quat_inv(a_gr), axis1));
a_lr = quat_mul(a_lr, quat_mul(r0, r2));
b_lr = quat_mul(b_lr, r1);
}
Bonus: Extension/Contraction Axis
The above code works perfectly in most cases, but can occasionally produce small popping artifacts when the leg is already almost fully extended. This is because the cross product used in the line vec3 axis0 = normalize(cross(c - a, b - a)); becomes unstable when the vectors c - a and b - a start to point in almost the same direction.
To make this computation more stable we can instead introduce an additional vector d which controls the axis on which we bend the joints during the first stage of extension/contraction:
if (use_stable_extension) {
vec3 axis0 = normalize(cross(c - a, d));
}
This axis d can be anything which is close to orthogonal to the vector from the hip to the foot, but it should usually be set to something like the direction in which the knee is pointing. For example, if your joints are oriented such that the Z axis is the forward facing direction you could compute it something like this:
vec3 d = quat_rotate(b_gr, vec3(0, 0, 1));This will then ensure that the extension and contraction phase always produces a rotation around the axis perpendicular to this and the vector from the hip to the foot - an axis which should remain stable no matter what the extension of the joint chain is like.