Encoding Events for Neural Networks

08/07/2021

One of the big advantages of using neural networks for generating animation in video games is that once a neural network has been trained, the animation data it was trained on can be thrown away, and the network used to generated the animation on-the-fly - potentially saving huge amounts of memory.

But when we start getting into the details, things start to get a bit more complicated. For example, there can be all kinds of meta-data that gets attached to animations in games such as tags or markups to label particular states or sections of an animation. There are also events, such as audio events, triggers, and synchronization points. We can even have things like pointers to other assets, comments, timestamps, and all sorts of other unstructured data. If we still want the benefit of throwing away all our animation data we need to encode all of this additional information in a way which is suitable for the neural network to generate at runtime.

Some of these are easier than others. If we have tags or markups associated with different ranges in the animation data we can use a one-hot encoding indicating the presence of each of these different tags at each frame, and train the network to output this additional one-hot vector along with the pose.

More tricky to encode are single frame events such as sound events, synchronization points, triggers, and other indicators. If we try to encode these as one-hot vectors as we did with the tags we have two problems: first, a problem of data imbalance as generally >99% of frames will not contain any events (and as such the neural network can achieve a fantastic accuracy by just ignoring this output altogether), and secondly, because we are only outputting a value at a single specific frame, we may find we miss or skip over an event if the frame-rate drops or the network does not make an accurate enough prediction.

So here is my little trick for encoding single frame events in a way which is far more suitable for neural networks:

The first step is to take your track of single frame events, and instead compute the signed time until the nearest event. So for example, if the nearest event is two seconds in the future you return 2, while if the nearest event was one that happened three seconds ago you return -3. Here is what this might look like visualized, where the single-frame events are shown in red and the signed time until the event is shown in blue:

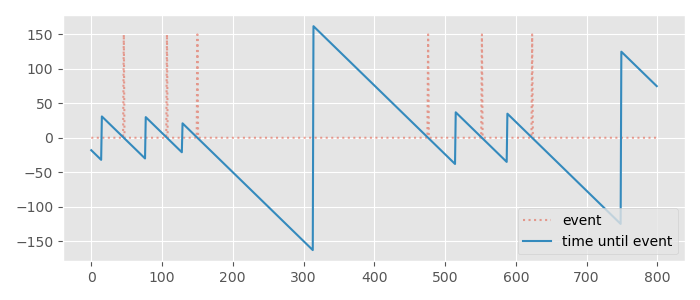
The intuition behind this transformation is that if we can have the network produce something like the signed time until the event we can trigger the event at the exact moment this output crosses zero. Using this encoding we can also apprehend events if need be by simply triggering the event a little before the output crosses zero. This can be useful for events such as sound or network events where we may need to prepare things a little bit in advance. Finally, since this value is not sparse, the network will not be able to simply ignore it as it would in the single-frame encoding.

However this encoding still has problems. Firstly, this value is unbounded - meaning we will be asking the network to produce a huge number when the nearest event is a very long time away, and secondly, we have a large discontinuity when the nearest event changes and we suddenly go from a large negative value to a large positive value.

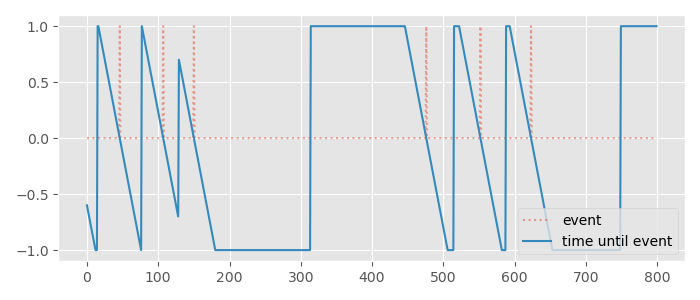
To fix the first issue we're going to clip this time to some maximum and minimum time - this is going to limit how much we can apprehend an event (or know how long it has been since an event) but it will mean the value is no longer unbounded, making it more suitable for prediction. For neatness we can also re-scale this into the range -1 to 1 by dividing by this maximum. Here I set the maximum to 30 frames.

To fix the second issue we're going to re-scale this again to the range \( -\pi \) to \( \pi \), treat it like an angle, and convert it to Cartesian coordinates using sin and cos:

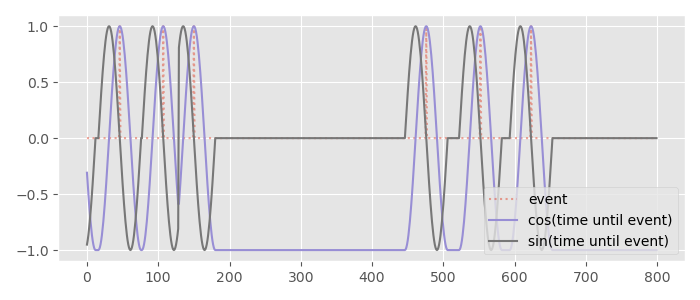
If you look closely you will see this has removed all discontinuities and encoded both the minimum time and maximum time as the same value. However, the gradient of this signal can still suddenly change, so I like to apply a tiny bit of Gaussian smoothing to make sure the resulting signal is nice and smooth:

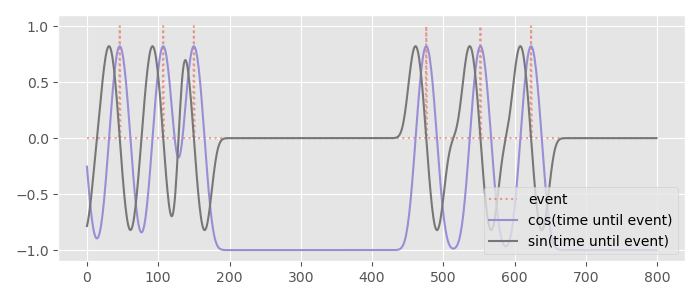
Now we have something that is non-sparse, bounded, smooth, and continuous - the perfect kind of signal for a neural network to predict.

Once trained, if we want to recover the original signed time until event again from our network prediction, all we need to do is apply the same operations in reverse: First, convert back from Cartesian coordinates to an angle using atan2, then re-scale back from the range \( -\pi \), \( \pi \) to the minimum time and maximum time, and voila! Here you can see a reconstruction of what that looks like compared to the original time until event:

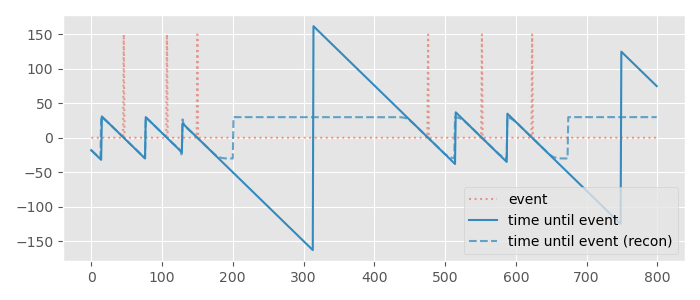
One thing you might notice about the reconstruction is that we need to treat the minimum time and maximum time as synonymous in meaning - both represent the same thing: that we don't know about the timing of the event because either it was too long ago, or it will happen at some point too far in the future. Similarly, we can see that our smoothing means we don't get exactly the right time predicted when the event is close to the maximum. But, we did preserve the fact that our prediction smoothly crosses zero at exactly when the event occurs which is more important.

Also important to know (although you cannot see it in this example) is that for events happening very frequently the time until event value can actually cross zero in the wrong direction when it is ramping up again. This means we need to be a little careful when we apprehend events: we should ignore the predicted time until event value completely when it is increasing rather than decreasing (and assume we don't know anything about the occurrence of the event). Similarly, when we check to see if we should trigger an event we need to make sure that the time until event value is crossing zero in the right direction (from positive to negative), moving at an appropriate speed, and in a relatively small range close to zero when doing so.

But other than those small caveats I've found this system to work remarkably well both for frequent events like foot contacts and also very sparse, long term events that only happen every so often. By controlling the maximum time and minimum time we can control how much apprehension is available vs how much precision is desired for the exact timing (I've found it's good to set this value to something close to the average period between events), and the whole thing only requires two additional outputs per event to be generated. Not bad!