Tags, Ranges and Masks
23/02/2022
Tags
I'm a big believer in the use of tags for organizing animation data. Tags provide a non-destructive, scalable, and flexible way to organize and structure data which can easily be accessed by in-game systems.
The core problem tags solve is one of implicit information. Standard ways of organizing animation data - files, folders, naming conventions, and other guidelines - are all either difficult, or even impossible to access and use from the game engine as structural information about the data is implicit in how the animation system was constructed, hidden away in the animator's heads, or spread out over random wiki pages.
For example, while animators commonly build sets of animations that are intended to be used together in the same blend space, for the engine to know this might require - at best - parsing a specific naming structure and folder hierarchy - or at worst - might simply be impossible.
Instead, if animations are given a tag which indicates their intended use, knowing this information is trivial. We can build game systems that do all sorts of interesting things - building blend spaces automatically, or performing testing and quality control checks for things like missing or incorrectly formed data for example.
And this example also highlights some important aspects of tagging which I think are often misunderstood:
- Tags are not semantic - they're not there to describe what is actually happening in the animations, but to provide some kind of logical hook for other systems which might want to know more about the data.
- Tags are cheap - There is no one-size-fits-all tagging of some data which will work with all problems. If two systems require tags with different structures, or levels of detail, then use two sets of tags.
- Tags are descriptive - The tags themselves don't do anything. They are simply another form of data to be consumed by game systems.
And while these points might sound obvious, I don't really think they are - and in many of the game engines I've worked with which supported tags, events, or other mark-up, they didn't always work like this.
For example, in many engines if you want an event to play a sound, it would be the event itself which triggers the sound, with a direct link to the sound file you actually want to play. The sound system itself is not the one asking the animation system if a "footstep" event happened during the last update.
The difference is subtle but important. For example, if we want to change the sound being played based on the terrain type below, then under one of these philosophies this requires relatively simple additional logic added to the sound system. While with the other, we might need to edit every footstep event to add this additional logic to its trigger.
The key difference here is in the separation of data and logic. Tags should be data, not logic. Because that gives us the freedom to easily change the logic later down the line if we want.
For example, rather than re-naming animation files using a particular naming scheme and putting them into a folder hierarchy, we could tag our files using tags that represent the same kind of description. And, rather than cutting animation files to particular lengths, we could instead use a tag to indicate the ranges we are interested in keeping.
Then, with tags, if we still want to use file naming schemes, folders, and cut up animation clips, we still can. All it takes is running an automatic process which looks at the tags and automatically performs the desired logic - cutting and re-naming files, putting them into the desired folder hierarchy.
But, if we change our minds later and want to do something else, we still can. Because by separating data and logic we keep this option open - unlike if we'd performed all this logic by hand.
Ranges
One generic way to represent tagged animations is using ranges - essentially start and stop frames for each tagged section that appears in each animation. Tags for whole animations can simply be given start and stop time corresponding to the entire length of the animation.
struct range
{
int start, stop;
};
Given this representation, one of the most powerful things we can do with tags is perform logical operations such as union, intersection, and difference - constructing arbitrary logical queries to find the sub-sections of our database which have the properties we want:
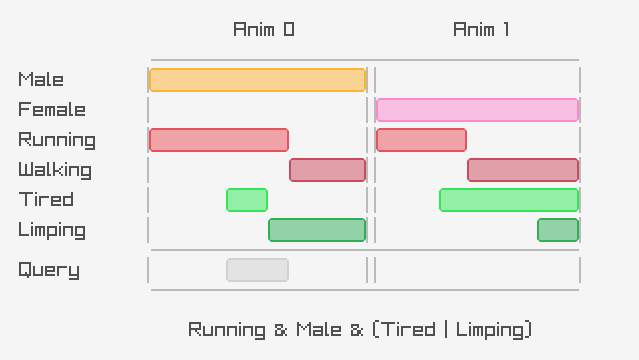
Not only does this provide a powerful, scalable way to examine and work with large amounts of animation data, but it can also be used by gameplay and AI systems at runtime. For example, we used this approach to dynamically filter the search domain of our Motion Matching system at runtime - effectively providing gameplay with a form of data-driven hard constraint they could use to limit the search to just the regions of the animations they were certain they wanted.
But the algorithm to actually compute such logical queries is not obvious at all on face value (to me at least).
The way to get an idea of how it might work is to consider the starts and stops of the ranges as a sorted series of events, which are to be processed in order, and the output ranges constructed on the fly according to the logical operations being performed:
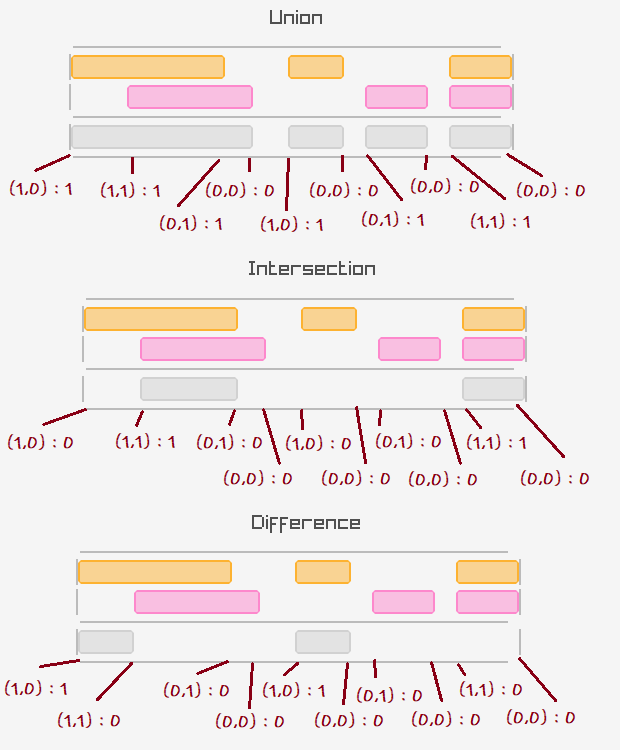
And here is how we actually implement something like this for the union operation - and brace yourself because there is a lot of code coming up:
// Process union operation on arrays of ranges.
// Assumes `out` is pre-allocated to be large enough
// to store result. Returns the number of ranges
// generated as output.
int ranges_union(
slice1d<range> out,
const slice1d<range> lhs,
const slice1d<range> rhs)
{
// Activation state of each list of ranges
bool out_active = false;
bool lhs_active = false;
bool rhs_active = false;
// Event index for each list of ranges
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// While both ranges have events to process
while (lhs_i < lhs.size * 2 && rhs_i < rhs.size * 2)
{
// Are the next lhs, and rhs events active or inactive
bool lhs_active_next = lhs_i % 2 == 0;
bool rhs_active_next = rhs_i % 2 == 0;
// Time of the next lhs, and rhs events
int lhs_t = lhs_active_next ? lhs(lhs_i / 2).start : lhs(lhs_i / 2).stop;
int rhs_t = rhs_active_next ? rhs(rhs_i / 2).start : rhs(rhs_i / 2).stop;
// Event from lhs is coming first
if (lhs_t < rhs_t)
{
// Activate output
if (!out_active && lhs_active_next)
{
out_active = true;
out(out_i).start = lhs_t;
}
// Deactivate output
else if (out_active && !lhs_active_next && !rhs_active)
{
out_active = false;
out(out_i).stop = lhs_t;
out_i++;
}
lhs_active = lhs_active_next;
lhs_i++;
}
// Event from rhs is coming first
else if (rhs_t < lhs_t)
{
// Activate output
if (!out_active && rhs_active_next)
{
out_active = true;
out(out_i).start = rhs_t;
}
// Deactivate output
else if (out_active && !lhs_active && !rhs_active_next)
{
out_active = false;
out(out_i).stop = rhs_t;
out_i++;
}
rhs_active = rhs_active_next;
rhs_i++;
}
// Event from lhs and rhs coming at same time
else
{
// Activate output
if (!out_active && (lhs_active_next || rhs_active_next))
{
out_active = true;
out(out_i).start = lhs_t;
}
// Deactivate output
else if (out_active && !(lhs_active_next || rhs_active_next))
{
out_active = false;
out(out_i).stop = lhs_t;
out_i++;
}
lhs_active = lhs_active_next;
rhs_active = rhs_active_next;
lhs_i++; rhs_i++;
}
}
// Process any remaining lhs events
while (lhs_i < lhs.size * 2)
{
bool lhs_active_next = lhs_i % 2 == 0;
int lhs_t = lhs_active_next ? lhs(lhs_i / 2).start : lhs(lhs_i / 2).stop;
// Activate output
if (!out_active && lhs_active_next)
{
out_active = true;
out(out_i).start = lhs_t;
}
// Deactivate output
else if (out_active && !lhs_active_next)
{
out_active = false;
out(out_i).stop = lhs_t;
out_i++;
}
lhs_active = lhs_active_next;
lhs_i++;
}
// Process any remaining rhs events
while (rhs_i < rhs.size * 2)
{
bool rhs_active_next = rhs_i % 2 == 0;
int rhs_t = rhs_active_next ? rhs(rhs_i / 2).start : rhs(rhs_i / 2).stop;
// Activate output
if (!out_active && rhs_active_next)
{
out_active = true;
out(out_i).start = rhs_t;
}
// Deactivate output
else if (out_active && !rhs_active_next)
{
out_active = false;
out(out_i).stop = rhs_t;
out_i++;
}
rhs_active = rhs_active_next;
rhs_i++;
}
// Return number of ranges added to output
return out_i;
}
Phew... but although the code may look intimidating, the basic concept is actually fairly simple and resembles the same pattern we would use to find the union of two sorted sets of integers. For each set of ranges we're effectively keeping an index on the next upcoming start or stop event (in this case using, lhs_i and rhs_i), and processing the incoming starts and stops, while constructing the resulting set of ranges on the fly based on the state of the two input ranges, lhs_active and rhs_active, and the output range out_active.
The implementation of intersection is a tiny bit simpler, since when either list of ranges runs out of events, we know we don't need to add any more ranges to generate the output.
// Process intersection operation on arrays of ranges.
// Assumes `out` is pre-allocated to be large enough
// to store result. Returns the number of ranges
// generated as output.
int ranges_intersection(
slice1d<range> out,
const slice1d<range> lhs,
const slice1d<range> rhs)
{
// Activation state of each list of ranges
bool out_active = false;
bool lhs_active = false;
bool rhs_active = false;
// Event index for each list of ranges
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// While both ranges have events to process
while (lhs_i < lhs.size * 2 && rhs_i < rhs.size * 2)
{
// Are the next lhs, and rhs events active or inactive
bool lhs_active_next = lhs_i % 2 == 0;
bool rhs_active_next = rhs_i % 2 == 0;
// Time of the next lhs, and rhs events
int lhs_t = lhs_active_next ? lhs(lhs_i / 2).start : lhs(lhs_i / 2).stop;
int rhs_t = rhs_active_next ? rhs(rhs_i / 2).start : rhs(rhs_i / 2).stop;
// Event from lhs coming first
if (lhs_t < rhs_t)
{
// Activate output
if (!out_active && rhs_active && lhs_active_next)
{
out_active = true;
out(out_i).start = lhs_t;
}
// Deactivate output
else if (out_active && !lhs_active_next)
{
out_active = false;
out(out_i).stop = lhs_t;
out_i++;
}
lhs_active = lhs_active_next;
lhs_i++;
}
// Event from rhs coming first
else if (rhs_t < lhs_t)
{
// Activate output
if (!out_active && lhs_active && rhs_active_next)
{
out_active = true;
out(out_i).start = rhs_t;
}
// Deactivate output
else if (out_active && !rhs_active_next)
{
out_active = false;
out(out_i).stop = rhs_t;
out_i++;
}
rhs_active = rhs_active_next;
rhs_i++;
}
// Event from lhs and rhs coming at same time
else
{
// Activate output
if (!out_active && (lhs_active_next && rhs_active_next))
{
out_active = true;
out(out_i).start = lhs_t;
}
// Deactivate output
else if (out_active && (!lhs_active_next || !rhs_active_next))
{
out_active = false;
out(out_i).stop = lhs_t;
out_i++;
}
lhs_active = lhs_active_next;
rhs_active = rhs_active_next;
lhs_i++; rhs_i++;
}
}
// Return number of ranges added to output
return out_i;
}
While the difference operation is again pretty similar, with the only unique aspect being that it is not symmetric like the others:
// Process difference operation on arrays of ranges.
// Assumes `out` is pre-allocated to be large enough
// to store result. Returns the number of ranges
// generated as output.
int ranges_difference(
slice1d<range> out,
const slice1d<range> lhs,
const slice1d<range> rhs)
{
// Activation state of each list of ranges
bool out_active = false;
bool lhs_active = false;
bool rhs_active = false;
// Event index for each list of ranges
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// While both ranges have events to process
while (lhs_i < lhs.size * 2 && rhs_i < rhs.size * 2)
{
// Are the next lhs, and rhs events active or inactive
bool lhs_active_next = lhs_i % 2 == 0;
bool rhs_active_next = rhs_i % 2 == 0;
// Time of the next lhs, and rhs events
int lhs_t = lhs_active_next ? lhs(lhs_i / 2).start : lhs(lhs_i / 2).stop;
int rhs_t = rhs_active_next ? rhs(rhs_i / 2).start : rhs(rhs_i / 2).stop;
// Event coming from lhs first
if (lhs_t < rhs_t)
{
// Activate output
if (!out_active && !rhs_active && lhs_active_next)
{
out_active = true;
out(out_i).start = lhs_t;
}
// Deactivate output
else if (out_active && !lhs_active_next)
{
out_active = false;
out(out_i).stop = lhs_t;
out_i++;
}
lhs_active = lhs_active_next;
lhs_i++;
}
// Event coming from rhs first
else if (rhs_t < lhs_t)
{
// Activate output
if (!out_active && lhs_active && !rhs_active_next)
{
out_active = true;
out(out_i).start = rhs_t;
}
// Deactivate output
else if (out_active && rhs_active_next)
{
out_active = false;
out(out_i).stop = rhs_t;
out_i++;
}
rhs_active = rhs_active_next;
rhs_i++;
}
// Event from lhs and rhs coming at same time
else
{
// Activate output
if (!out_active && lhs_active_next && !rhs_active_next)
{
out_active = true;
out(out_i).start = lhs_t;
}
// Deactivate output
else if (out_active && rhs_active_next)
{
out_active = false;
out(out_i).stop = lhs_t;
out_i++;
}
lhs_active = lhs_active_next;
rhs_active = rhs_active_next;
lhs_i++; rhs_i++;
}
}
// Process any remaining lhs events
while (lhs_i < lhs.size * 2)
{
bool lhs_active_next = lhs_i % 2 == 0;
int lhs_t = lhs_active_next ? lhs(lhs_i / 2).start : lhs(lhs_i / 2).stop;
// Activate output
if (!out_active && lhs_active_next)
{
out_active = true;
out(out_i).start = lhs_t;
}
// Deactivate output
else if (out_active && !lhs_active_next)
{
out_active = false;
out(out_i).stop = lhs_t;
out_i++;
}
lhs_active = lhs_active_next;
lhs_i++;
}
// Return number of ranges added to output
return out_i;
}
Sets
These functions actually only solve half of our problem, because in reality we have multiple different animations, each with their own set of ranges that should be processed according to whatever logical operation we are performing. To handle this I like to use what I call a range_set - a single object that stores a set of ranges for multiple animations:
struct range_set
{
array1d<int> anims; // Sorted ids of all anims with ranges in set
array1d<range> anims_subranges; // Slices of `ranges` array for each anim
array1d<range> ranges; // Full list of all ranges for all animations
};
Here, ranges is the list of all the different ranges in this set, anims is a list of all the animation ids which have ranges in this set - then anims_subranges actually describes not ranges in the animations, but the slices of the ranges array which correspond to each animation listed in anims.
This structure might seem odd, but essentially I've just packed together all the ranges into a single array, and recorded the animations those ranges actually correspond to using anims_subranges and anims. Although perhaps not the most simple way you can set this up, it works well at removing the additional indirection and memory fragmentation we might get if we stored each animation's ranges in a separate array (some of which may have very few elements).
To perform logical operations on these range_set objects we actually follow a similar pattern to what we used before: given two range sets we iterate over each of their anims arrays in order, and construct the output set on the fly. For example, for the union operation, if we find an animation in one set but not other we simply add all the corresponding ranges to the output, while if we find an animation in both sets, we need to find the range union of those two sets of ranges and add that. In code it looks something like this:
void range_set_union(
range_set& out,
const range_set& lhs,
const range_set& rhs)
{
// Allocate potential maximum number of anims and ranges we might to output
out.anims.resize(lhs.anims.size + rhs.anims.size);
out.anims_subranges.resize(lhs.anims.size + rhs.anims.size);
out.ranges.resize(lhs.ranges.size + rhs.ranges.size);
// Anim index for each list of ranges
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// Output ranges index
int ranges_i = 0;
// While both sets have animations
while (lhs_i < lhs.anims.size && rhs_i < rhs.anims.size)
{
// If animation from lhs is first
if (lhs.anims(lhs_i) < rhs.anims(rhs_i))
{
// Append subranges to output
slice1d<range> sranges = lhs.ranges.slice(lhs.anims_subranges(lhs_i));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + sranges.size };
out.ranges.slice(ranges_i, ranges_i + sranges.size) = sranges;
ranges_i+=sranges.size;
out_i++;
lhs_i++;
}
// If animation from rhs is first
else if (rhs.anims(rhs_i) < lhs.anims(lhs_i))
{
// Append subranges to output
slice1d<range> sranges = rhs.ranges.slice(rhs.anims_subranges(rhs_i));
out.anims(out_i) = rhs.anims(rhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + sranges.size };
out.ranges.slice(ranges_i, ranges_i + sranges.size) = sranges;
ranges_i+=sranges.size;
out_i++;
rhs_i++;
}
// If both contain the same animation
else
{
// Append union of subranges to output
int nranges = ranges_union(
out.ranges.slice_from(ranges_i),
lhs.ranges.slice(lhs.anims_subranges(lhs_i)),
rhs.ranges.slice(rhs.anims_subranges(rhs_i)));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + nranges };
ranges_i+=nranges;
out_i++;
lhs_i++; rhs_i++;
}
}
// Process any remaining lhs animations
while (lhs_i < lhs.anims.size)
{
// Append subranges to output
slice1d<range> sranges = lhs.ranges.slice(lhs.anims_subranges(lhs_i));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + sranges.size };
out.ranges.slice(ranges_i, ranges_i + sranges.size) = sranges;
ranges_i+=sranges.size;
out_i++;
lhs_i++;
}
// Process any remaining rhs animations
while (rhs_i < rhs.anims.size)
{
// Append subranges to output
slice1d<range> sranges = rhs.ranges.slice(rhs.anims_subranges(rhs_i));
out.anims(out_i) = rhs.anims(rhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + sranges.size };
out.ranges.slice(ranges_i, ranges_i + sranges.size) = sranges;
ranges_i+=sranges.size;
out_i++;
rhs_i++;
}
// Resize output to match what was added
out.anims.resize(out_i);
out.anims_subranges.resize(out_i);
out.ranges.resize(ranges_i);
}
Similar functions can be defined for intersection:
void range_set_intersection(
range_set& out,
const range_set& lhs,
const range_set& rhs)
{
// Allocate potential maximum number of anims and ranges we might to output
out.anims.resize(lhs.anims.size + rhs.anims.size);
out.anims_subranges.resize(lhs.anims.size + rhs.anims.size);
out.ranges.resize(lhs.ranges.size + rhs.ranges.size);
// Anim index for each list of ranges
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// Output ranges index
int ranges_i = 0;
// While both sets have animations
while (lhs_i < lhs.anims.size && rhs_i < rhs.anims.size)
{
// If animation is in lhs but not rhs skip
if (lhs.anims(lhs_i) < rhs.anims(rhs_i))
{
lhs_i++;
}
// If animation is in rhs but not lhs skip
else if (rhs.anims(rhs_i) < lhs.anims(lhs_i))
{
rhs_i++;
}
// If animation is in both lhs and rhs
else
{
// Append intersection of subranges to output
int nranges = ranges_intersection(
out.ranges.slice_from(ranges_i),
lhs.ranges.slice(lhs.anims_subranges(lhs_i)),
rhs.ranges.slice(rhs.anims_subranges(rhs_i)));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + nranges };
ranges_i+=nranges;
out_i++;
lhs_i++; rhs_i++;
}
}
// Resize output to match what was added
out.anims.resize(out_i);
out.anims_subranges.resize(out_i);
out.ranges.resize(ranges_i);
}
And difference:
void range_set_difference(
range_set& out,
const range_set& lhs,
const range_set& rhs)
{
// Allocate potential maximum number of anims and ranges we might to output
out.anims.resize(lhs.anims.size + rhs.anims.size);
out.anims_subranges.resize(lhs.anims.size + rhs.anims.size);
out.ranges.resize(lhs.ranges.size + rhs.ranges.size);
// Anim index for each list of ranges
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// Output ranges index
int ranges_i = 0;
// While both sets have animations
while (lhs_i < lhs.anims.size && rhs_i < rhs.anims.size)
{
// If animation from lhs is first
if (lhs.anims(lhs_i) < rhs.anims(rhs_i))
{
slice1d<range> sranges = lhs.ranges.slice(lhs.anims_subranges(lhs_i));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + sranges.size };
out.ranges.slice(ranges_i, ranges_i + sranges.size) = sranges;
ranges_i+=sranges.size;
out_i++;
lhs_i++;
}
// If animation is in rhs but not lhs skip
else if (rhs.anims(rhs_i) < lhs.anims(lhs_i))
{
rhs_i++;
}
// If animation is in both lhs and rhs
else
{
// Append difference of subranges to output
int nranges = ranges_difference(
out.ranges.slice_from(ranges_i),
lhs.ranges.slice(lhs.anims_subranges(lhs_i)),
rhs.ranges.slice(rhs.anims_subranges(rhs_i)));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + nranges };
ranges_i+=nranges;
out_i++;
lhs_i++; rhs_i++;
}
}
// Process any remaining lhs animations
while (lhs_i < lhs.anims.size)
{
slice1d<range> sranges = lhs.ranges.slice(lhs.anims_subranges(lhs_i));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_subranges(out_i) = { ranges_i, ranges_i + sranges.size };
out.ranges.slice(ranges_i, ranges_i + sranges.size) = sranges;
ranges_i+=sranges.size;
out_i++;
lhs_i++;
}
// Resize output to match what was added
out.anims.resize(out_i);
out.anims_subranges.resize(out_i);
out.ranges.resize(ranges_i);
}
While it does feel like a lot of code, to be honest I find this pattern kind of a neat. The idea that if we have two sorted lists of things, we can iterate over the union, intersection, or difference on those things just by iterating over them together in order is a nice little trick that is often forgotten or only used by specific data structures.
Also, these range_set objects actually act like a kind of acceleration structure when doing our logical operations - allowing us to copy over or discard a whole bunch of ranges without going into the real, fine-grained union, intersection, or difference operations.
These functions can already be used for computing various logical queries on range sets, but I like to also introduce a separate object we can use to actually build up a logical query without evaluating it. Here the basic idea is to build our query using a stack of integers, where negative integers represent operations, and positive integers represent some set index (for which the actual set will be provided during evaluation).
// Query operations encoded by negative numbers
enum
{
QUERY_OP_UNION = -1,
QUERY_OP_INTERSECTION = -2,
QUERY_OP_DIFFERENCE = -3
};
// Query expr object consists of a stack of set
// indices and logical operations
struct query_expr
{
// Construct empty expression
query_expr() {}
// Construct from a single set index
query_expr(int set) : stack(1) { stack(0) = set; }
// Construct from two other range set queries and an op
query_expr(
const query_expr& lhs,
const query_expr& rhs,
int op)
: stack(lhs.stack.size + rhs.stack.size + 1)
{
// Assert op is negative
assert(op < 0);
// Copy rhs and lhs into stack
stack.slice(0, rhs.stack.size) = rhs.stack;
stack.slice(rhs.stack.size, rhs.stack.size + lhs.stack.size) = lhs.stack;
// Put op on top
stack(stack.size - 1) = op;
}
// Inplace array used to store stack - can store
// up to 16 elements without using heap allocation
inplace_array1d<int, 16> stack;
};
One nice little trick here is to use an inplace_array1d<int, 16>, which is essentially an array object which pre-allocates a certain number of elements to avoid using heap allocation when the number of elements is small. In this case it allows us to build up expressions of up to 16 elements without performing any dynamic memory allocation, which in most cases should be plenty.
Since this object is much smaller, and more simple than our range set object it makes a bit more sense to overload some operators for it so we can have nice syntax:
query_expr operator|(const query_expr& lhs, const query_expr& rhs)
{
return query_expr(lhs, rhs, QUERY_OP_UNION);
}
query_expr operator&(const query_expr& lhs, const query_expr& rhs)
{
return query_expr(lhs, rhs, QUERY_OP_INTERSECTION);
}
query_expr operator-(const query_expr& lhs, const query_expr& rhs)
{
return query_expr(lhs, rhs, QUERY_OP_DIFFERENCE);
}
Now we can construct logical queries in code with the syntax we might expect:
query_expr Male(tag_index(tag_names, "Male"));
query_expr Female(tag_index(tag_names, "Female"));
query_expr Running(tag_index(tag_names, "Running"));
query_expr Walking(tag_index(tag_names, "Walking"));
query_expr Tired(tag_index(tag_names, "Tired"));
query_expr Limping(tag_index(tag_names, "Limping"));
query_expr query = Running & Male & (Tired | Limping);
To evaluate this query, we just move down the stack and perform the operations it encodes:
// Recursively evaluate range set query by
// walking down the stack from top to bottom
// and performing the operations encoded by them
void query_expr_evaluate_range_set_from(
range_set& out,
int& index,
const query_expr& query,
const std::vector<range_set>& range_sets)
{
range_set lhs, rhs;
switch (query.stack(index))
{
case QUERY_OP_UNION:
index--;
query_expr_evaluate_range_set_from(lhs, index, query, range_sets);
query_expr_evaluate_range_set_from(rhs, index, query, range_sets);
range_set_union(out, lhs, rhs);
break;
case QUERY_OP_INTERSECTION:
index--;
query_expr_evaluate_range_set_from(lhs, index, query, range_sets);
query_expr_evaluate_range_set_from(rhs, index, query, range_sets);
range_set_intersection(out, lhs, rhs);
break;
case QUERY_OP_DIFFERENCE:
index--;
query_expr_evaluate_range_set_from(lhs, index, query, range_sets);
query_expr_evaluate_range_set_from(rhs, index, query, range_sets);
range_set_difference(out, lhs, rhs);
break;
default:
out = range_sets[query.stack(index)];
index--;
break;
}
}
void query_expr_evaluate_range_set(
range_set& out,
const query_expr& query,
const std::vector<range_set>& range_sets)
{
// If empty query, return empty range set
if (query.stack.size == 0)
{
out = range_set();
}
else
{
// Start at top of stack and evaluate
int index = query.stack.size - 1;
query_expr_evaluate_range_set_from(out, index, query, range_sets);
// Assert we've consumed all of the stack
assert(index == -1);
}
}
Notice how we need to pass in a vector of range_set objects so that the evaluation knows what each set index corresponds to.
Having a compact, simple representation of query objects has another benefit - we can use the query object as a key in a hashtable and cache the result of the evaluation, which, although not crazily expensive, we still probably want to avoid re-running every single frame if possible:
// Quick and dirty hash function
size_t memhash(const void* ptr, size_t num)
{
size_t h = 0x7A99ED;
for (int i = 0; i < num; i++)
{
h = (h * 54059) ^ (((const char*)ptr)[i] * 76963);
}
return h;
}
// Hash function for queries
struct query_expr_hash
{
size_t operator()(const query_expr& x) const
{
return memhash(x.stack.data, sizeof(int) * x.stack.size);
}
};
// Comparison function for queries
struct query_expr_cmp
{
bool operator()(const query_expr& lhs, const query_expr& rhs) const
{
if (lhs.stack.size == rhs.stack.size)
{
return memcmp(
lhs.stack.data,
rhs.stack.data,
sizeof(int) * lhs.stack.size) == 0;
}
else
{
return false;
}
}
};
// Hashtable to cache range set evaluations
using query_expr_range_set_cache = std::unordered_map<
query_expr,
range_set,
query_expr_hash,
query_expr_cmp>;
Then at runtime...
query_expr_range_set_cache range_cache;
query_expr query;
range_set query_range_set;
/* Later on... */
auto lookup = range_cache.find(query);
if (lookup != range_cache.end())
{
query_range_set = lookup->second;
}
else
{
query_expr_evaluate_range_set(query_range_set, query, tag_range_sets);
range_cache[query] = query_range_set;
}
And with that we have a pretty nice system for doing logical queries on tags!
Rasterization & Vectorization
There is another option for processing ranges, which is to rasterize them - essentially rendering them out to a long bitmask array where we use one bit to say if that tag is active or not for every frame of animation. Here I'm using an array-like object slice1d_bit which essentially acts like a slice of an array of single bits:
void ranges_rasterize(
slice1d_bit out,
const slice1d<range> ranges)
{
// Zero out all bits
out.zero();
for (int i = 0; i < ranges.size; i++)
{
// Write ones for range
out.slice(ranges(i)).one();
}
}
With this representation logical operations are pretty straight forward:
void mask_union(
slice1d_bit out,
const slice1d_bit lhs,
const slice1d_bit rhs)
{
assert((out.size == lhs.size) && (out.size == rhs.size));
for (int i = 0; i < out.size; i++)
{
out.set(i, lhs.get(i) || rhs.get(i));
}
}
void mask_intersection(
slice1d_bit out,
const slice1d_bit lhs,
const slice1d_bit rhs)
{
assert((out.size == lhs.size) && (out.size == rhs.size));
for (int i = 0; i < out.size; i++)
{
out.set(i, lhs.get(i) && rhs.get(i));
}
}
void mask_difference(
slice1d_bit out,
const slice1d_bit lhs,
const slice1d_bit rhs)
{
assert((out.size == lhs.size) && (out.size == rhs.size));
for (int i = 0; i < out.size; i++)
{
out.set(i, lhs.get(i) && !rhs.get(i));
}
}
which also means we can write custom functions to do specific queries with relative ease:
void mask_custom_logic(
slice1d_bit query,
const slice1d_bit running,
const slice1d_bit male,
const slice1d_bit tired,
const slice1d_bit limping)
{
for (int i = 0; i < query.size; i++)
{
query.set(i,
running.get(i) && male.get(i) && (tired.get(i) || limping.get(i)));
}
}
To convert back into ranges or vectorize, we simply find the points where the bitmask changes from inactive to active and back:
// Converts a mask into a set of ranges, assumes
// `out` is pre-allocated to be large enough to
// store result. Returns number of ranges added.
int mask_vectorize(
slice1d<range> out,
const slice1d_bit mask)
{
bool out_active = false;
int out_i = 0;
for (int i = 0; i < mask.size; i++)
{
// Activate output
if (!out_active && mask.get(i))
{
out(out_i).start = i;
out_active = true;
}
// Deactivate output
else if (out_active && !mask.get(i))
{
out(out_i).stop = i;
out_active = false;
out_i++;
}
}
// Deactivate output
if (out_active)
{
out(out_i).stop = mask.size;
out_i++;
}
return out_i;
}
Like before, if we want to store these for different animations we can do so with a similar structure, which we'll call a mask_set:
struct mask_set
{
array1d<int> anims; // Sorted ids of all anims with masks in set
array1d<range> anims_submasks; // Slices of `masks` array for each anim
array1d_bit masks; // Full list of all masks for all animations
};
Where the functions to perform logical operations on these are pretty much identical to the ones we used for ranges:
void mask_set_union(
mask_set& out,
const mask_set& lhs,
const mask_set& rhs)
{
// Allocate potential maximum number of anims and ranges we might to output
out.anims.resize(lhs.anims.size + rhs.anims.size);
out.anims_submasks.resize(lhs.anims.size + rhs.anims.size);
out.masks.resize(lhs.masks.size + rhs.masks.size);
// Anim index for each list of masks
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// Output masks index
int masks_i = 0;
// While both sets have animations
while (lhs_i < lhs.anims.size && rhs_i < rhs.anims.size)
{
// If animation from lhs is first
if (lhs.anims(lhs_i) < rhs.anims(rhs_i))
{
// Append submask to output
slice1d_bit submask = lhs.masks.slice(lhs.anims_submasks(lhs_i));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + submask.size };
out.masks.slice(masks_i, masks_i + submask.size) = submask;
masks_i+=submask.size;
out_i++;
lhs_i++;
}
// If animation from rhs is first
else if (rhs.anims(rhs_i) < lhs.anims(lhs_i))
{
// Append submask to output
slice1d_bit submask = rhs.masks.slice(rhs.anims_submasks(rhs_i));
out.anims(out_i) = rhs.anims(rhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + submask.size };
out.masks.slice(masks_i, masks_i + submask.size) = submask;
masks_i+=submask.size;
out_i++;
rhs_i++;
}
// If both contain the same animation
else
{
// Append union of submask to output
int nmasks = lhs.masks.slice(lhs.anims_submasks(lhs_i)).size;
mask_union(
out.masks.slice(masks_i, masks_i + nmasks),
lhs.masks.slice(lhs.anims_submasks(lhs_i)),
rhs.masks.slice(rhs.anims_submasks(rhs_i)));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + nmasks };
masks_i+=nmasks;
out_i++;
lhs_i++; rhs_i++;
}
}
// Process any remaining lhs animations
while (lhs_i < lhs.anims.size)
{
// Append submask to output
slice1d_bit submask = lhs.masks.slice(lhs.anims_submasks(lhs_i));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + submask.size };
out.masks.slice(masks_i, masks_i + submask.size) = submask;
masks_i+=submask.size;
out_i++;
lhs_i++;
}
// Process any remaining rhs animations
while (rhs_i < rhs.anims.size)
{
// Append submask to output
slice1d_bit submask = rhs.masks.slice(rhs.anims_submasks(rhs_i));
out.anims(out_i) = rhs.anims(rhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + submask.size };
out.masks.slice(masks_i, masks_i + submask.size) = submask;
masks_i+=submask.size;
out_i++;
rhs_i++;
}
// Resize output to match what was added
out.anims.resize(out_i);
out.anims_submasks.resize(out_i);
out.masks.resize(masks_i);
}
void mask_set_intersection(
mask_set& out,
const mask_set& lhs,
const mask_set& rhs)
{
// Allocate potential maximum number of anims and masks we might to output
out.anims.resize(lhs.anims.size + rhs.anims.size);
out.anims_submasks.resize(lhs.anims.size + rhs.anims.size);
out.masks.resize(lhs.masks.size + rhs.masks.size);
// Anim index for each list of masks
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// Output masks index
int masks_i = 0;
// While both sets have animations
while (lhs_i < lhs.anims.size && rhs_i < rhs.anims.size)
{
// If animation is in lhs but not rhs skip
if (lhs.anims(lhs_i) < rhs.anims(rhs_i))
{
lhs_i++;
}
// If animation is in rhs but not lhs skip
else if (rhs.anims(rhs_i) < lhs.anims(lhs_i))
{
rhs_i++;
}
// If animation is in both lhs and rhs
else
{
// Append intersection of submask to output
int nmasks = lhs.masks.slice(lhs.anims_submasks(lhs_i)).size;
mask_intersection(
out.masks.slice(masks_i, masks_i + nmasks),
lhs.masks.slice(lhs.anims_submasks(lhs_i)),
rhs.masks.slice(rhs.anims_submasks(rhs_i)));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + nmasks };
masks_i+=nmasks;
out_i++;
lhs_i++; rhs_i++;
}
}
// Resize output to match what was added
out.anims.resize(out_i);
out.anims_submasks.resize(out_i);
out.masks.resize(masks_i);
}
void mask_set_difference(
mask_set& out,
const mask_set& lhs,
const mask_set& rhs)
{
// Allocate potential maximum number of anims and ranges we might to output
out.anims.resize(lhs.anims.size + rhs.anims.size);
out.anims_submasks.resize(lhs.anims.size + rhs.anims.size);
out.masks.resize(lhs.masks.size + rhs.masks.size);
// Anim index for each list of masks
int out_i = 0;
int lhs_i = 0;
int rhs_i = 0;
// Output masks index
int masks_i = 0;
// While both sets have animations
while (lhs_i < lhs.anims.size && rhs_i < rhs.anims.size)
{
// If animation from lhs is first
if (lhs.anims(lhs_i) < rhs.anims(rhs_i))
{
slice1d_bit submask = lhs.masks.slice(lhs.anims_submasks(lhs_i));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + submask.size };
out.masks.slice(masks_i, masks_i + submask.size) = submask;
masks_i+=submask.size;
out_i++;
lhs_i++;
}
// If animation is in rhs but not lhs skip
else if (rhs.anims(rhs_i) < lhs.anims(lhs_i))
{
rhs_i++;
}
// If animation is in both lhs and rhs
else
{
// Append difference of submask to output
int nmasks = lhs.masks.slice(lhs.anims_submasks(lhs_i)).size;
mask_difference(
out.masks.slice(masks_i, masks_i + nmasks),
lhs.masks.slice(lhs.anims_submasks(lhs_i)),
rhs.masks.slice(rhs.anims_submasks(rhs_i)));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + nmasks };
masks_i+=nmasks;
out_i++;
lhs_i++; rhs_i++;
}
}
// Process any remaining lhs animations
while (lhs_i < lhs.anims.size)
{
slice1d_bit submask = lhs.masks.slice(lhs.anims_submasks(lhs_i));
out.anims(out_i) = lhs.anims(lhs_i);
out.anims_submasks(out_i) = { masks_i, masks_i + submask.size };
out.masks.slice(masks_i, masks_i + submask.size) = submask;
masks_i+=submask.size;
out_i++;
lhs_i++;
}
// Resize output to match what was added
out.anims.resize(out_i);
out.anims_submasks.resize(out_i);
out.masks.resize(masks_i);
}
Which we can even re-use along with our query object:
void query_expr_evaluate_mask_set_from(
mask_set& out,
int& index,
const query_expr& query,
const std::vector<mask_set>& mask_sets)
{
mask_set lhs, rhs;
switch (query.stack(index))
{
case QUERY_OP_UNION:
index--;
query_expr_evaluate_mask_set_from(lhs, index, query, mask_sets);
query_expr_evaluate_mask_set_from(rhs, index, query, mask_sets);
mask_set_union(out, lhs, rhs);
break;
case QUERY_OP_INTERSECTION:
index--;
query_expr_evaluate_mask_set_from(lhs, index, query, mask_sets);
query_expr_evaluate_mask_set_from(rhs, index, query, mask_sets);
mask_set_intersection(out, lhs, rhs);
break;
case QUERY_OP_DIFFERENCE:
index--;
query_expr_evaluate_mask_set_from(lhs, index, query, mask_sets);
query_expr_evaluate_mask_set_from(rhs, index, query, mask_sets);
mask_set_difference(out, lhs, rhs);
break;
default:
out = mask_sets[query.stack(index)];
index--;
break;
}
}
void query_expr_evaluate_mask_set(
mask_set& out,
const query_expr& query,
const std::vector<mask_set>& mask_sets)
{
if (query.stack.size == 0)
{
out = mask_set();
}
else
{
int index = query.stack.size - 1;
query_expr_evaluate_mask_set_from(out, index, query, mask_sets);
assert(index == -1);
}
}
And our cache:
// Hashtable to cache mask set evaluations
using query_expr_mask_set_cache = std::unordered_map<
query_expr,
mask_set,
query_expr_hash,
query_expr_cmp>;
Which representation works better in terms of memory and performance depends a lot on the context - but we can get an idea by thinking about the information density. Given that a single range requires at least two, 32-bit integers to store (although we could probably use 16-bit integers instead if we wanted), we can estimate that if we have many small ranges less than 64 frames in length, we will probably be saving memory and achieving better performance by using the rasterized masks instead. Whereas if we have just a few, very long ranges, then we would expect the vectorized versions to perform a lot better.
But logically, they perform identically, as you can see here, with exactly the same setup but using masks instead of ranges under the hood:
Conclusion
Tagging is a nice way to organize and structure animation data which is non-destructive and allows for all sorts of interesting operations such as the querying shown here. These are the most complex operations, but there are others that are probably interesting to implement too, such as taking just the first or last N frames in a set of ranges, filtering out ranges greater than or less than some length, taking the first range from a set of ranges, or perhaps even a random range from a set of ranges.
However tagging is also not an entirely perfect solution. I used integer ranges in this post, but if you use float ranges you may well need to be careful to avoid accumulating floating point error, or introduce very short (or even negative in length) ranges. It can also be difficult to work out how to aggregate additional data associated with ranges during these logical queries. In fact, I would consider treating any data attached to a range more like a property of the underlying frames of animation, rather than something tied to the range object itself.
Tags can also be a lot of manual labor to add. And while I would argue that this manual processing is usually being performed elsewhere anyway as part of the data processing (such as in clipping or re-naming files) - one thing that is certain is that relying on tags means relying on a good and efficient tagging tool.
Finally, tags can suffer from things like naming collisions, and there is still of course the difficult issue of deciding on the names of everything. Here things like multiple tagging sets, or tagging namespaces can help.
Overall, I hope this post has been interesting and helpful, and perhaps made more clear some algorthms which I believe are not obvious without a bit of investigation, but can be very powerful when combined with tags.
Demo & Source Code
If you'd like to play around with trying different logical queries, you can try an interactive demo here. Or if you want to check out the source code for this article in more detail you can find it here.