Dead Blending
25/02/2023
I recently learned from some colleagues about a different approach to inertialization sometimes called "dead blending" (due to its resemblance to dead reckoning) and thought it would be fun to try it out.
The basic idea is this: instead of storing an offset between source and destination animations which we fade out, we instead extrapolate forward in time the source animation clip past the point of transition, and insert a normal cross-fade blend between the extrapolated source clip and the destination clip.
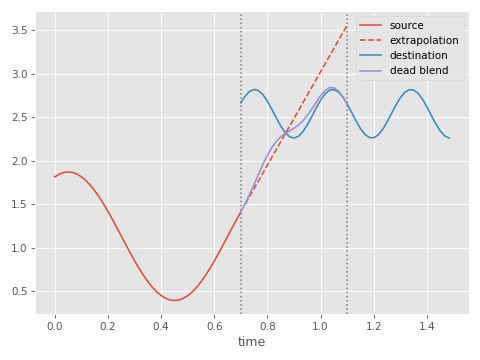
This can be implemented easily. At transition time we simply record the position and velocity of the currently playing animation, and reset the blend timer:
void dead_blending_transition(
float& ext_x, // Extrapolated position
float& ext_v, // Extrapolated velocity
float& ext_t, // Time since transition
float src_x, // Current position
float src_v) // Current velocity
{
ext_x = src_x;
ext_v = src_v;
ext_t = 0.0f;
}Then on update we extrapolate the recorded animation forward (by integrating the velocity) and blend it with our now playing animation.
void dead_blending_update(
float& out_x, // Output position
float& out_v, // Output velocity
float& ext_x, // Extrapolated position
float& ext_v, // Extrapolated velocity
float& ext_t, // Time since transition
float in_x, // Input position
float in_v, // Input velocity
float blendtime, // Blend time
float dt, // Delta time
float eps=1e-8f)
{
if (ext_t < blendtime)
{
ext_x += ext_v * dt;
ext_t += dt;
float alpha = smoothstep(ext_t / max(blendtime, eps));
out_x = lerp(ext_x, in_x, alpha);
out_v = lerp(ext_v, in_v, alpha);
}
else
{
out_x = in_x;
out_v = in_v;
}
}
This is what it looks like:
Applying it to a whole character is not much more difficult. We can linearly extrapolate each joint in the same way:
void extrapolate_linear(
slice1d<vec3> bone_positions,
slice1d<vec3> bone_velocities,
slice1d<quat> bone_rotations,
slice1d<vec3> bone_angular_velocities,
const float dt = 1.0f / 60.0f)
{
for (int i = 0; i < bone_positions.size; i++)
{
bone_positions(i) = bone_positions(i) + dt * bone_velocities(i);
bone_rotations(i) = quat_mul(
quat_from_scaled_angle_axis(dt * bone_angular_velocities(i)),
bone_rotations(i));
}
}
And then use whatever our preferred blending algorithm is such as using lerp on positions and slerp on rotations.
One thing we need to be careful of is the blend "switching sides". Because the extrapolated pose can end up very different to the animation we are feeding as input, sometimes the "shortest rotation" between these two poses can suddenly change i.e. from a rotation of +175 degrees to a rotation of -175 degrees, causing pops or jitters.
Here is a slight variation of the slerp function that avoids that by keeping track of the current blend direction d and sticking with it. Then all we need to do is reset d to the identity rotation on transition.
quat quat_slerp_via(quat q, quat p, quat& d, float alpha, float eps=1e-5f)
{
// Find shortest path between the two
// quaternions we want to blend
quat e = quat_abs(quat_mul_inv(p, q));
// Check if shortest path is on the same
// hemisphere as path given by quaternion d
if (quat_dot(d, e) < 0.0f)
{
// If not, we go the other way around to
// match the path described by d
e = -e;
}
// Update d to match our current path
d = e;
// Rotate along our current path
return quat_mul(quat_exp(quat_log(e) * alpha), q);
}
Here is what this looks like when used in our little Motion Matching demo (I've turned IK off in all these demos to better evaluate the results):
Although the result is not perfect, what I really like about dead-blending is its simplicity. The offset-based inertializer is not exactly complicated, but it requires both the source and destination animations to be evaluated (and their velocities) on the frame of transition. This is something which is not always easy in all existing animation systems. Dead-blending only requires that you have the current pose, which should pretty much always be available, and (at the point of transition) its velocity, which can be tracked with finite difference if need be.
The cross fade blend also means the resulting animation will always be something in-between the extrapolated source animation and the destination animation. In theory, this should help prevent many of the artifacts we see from offset-based inertial blending such as knee pops and floaty, swimming motions.
It does however, end up damping out some of the details of the destination clip, and as we saw in the spring environment, can sometimes produce weird movements. We can also get foot-sliding and the general feeling of mushiness that bad cross-fade blends can introduce (although this is greatly improved by the fact we only ever blend two animations at a time).
Perhaps the bigger problem with this very simple implementation is that if we don't use a very short blend time the extrapolation of the source animation can very quickly produce crazy poses which (even with a low weight) can be an issue. For example, here is what a linear extrapolation of a pose looks like if we run it for a full second:
And although one second is an unrealistically long blend time, even for a normal blend time of something like 0.2 seconds, if we look carefully we can still see jittery motion, over and under rotation, and the other issues that this introduces:
We can avoid creating crazy poses somewhat by decaying the pose velocities using a damper, which in our springs environment we could implement something like this:
float damper_decay_exact(float x, float halflife, float dt, float eps=1e-5f)
{
return x * fast_negexp((0.69314718056f * dt) / (halflife + eps));
}
void dead_blending_update_decay(
float& out_x, // Output position
float& out_v, // Output velocity
float& ext_x, // Extrapolated position
float& ext_v, // Extrapolated velocity
float& ext_t, // Time since transition
float in_x, // Input position
float in_v, // Input velocity
float blendtime, // Blend time
float decay_halflife, // Decay Halflife
float dt, // Delta time
float eps=1e-8f)
{
if (ext_t < blendtime)
{
ext_v = damper_decay_exact(ext_v, decay_halflife, dt);
ext_x += ext_v * dt;
ext_t += dt;
float alpha = smoothstep(ext_t / max(blendtime, eps));
out_x = lerp(ext_x, in_x, alpha);
out_v = lerp(ext_v, in_v, alpha);
}
else
{
out_x = in_x;
out_v = in_v;
}
}
This stops the extrapolations going quite so crazy and produces poses that visually look a little more sane:
It also appears to do a good job of removing some of the jitters, although we still see some shakes and other odd movements from time to time:
One thing we can try is limiting the extrapolation to be within the bounds of some joint limits. Here is what things looks like if we clamp the extrapolation in this way.
Alternatively, we can bounce the animation off the joint limits. This is done by adding a velocity pushing away from the limit, whenever the joint limit is violated:
To me these extrapolations look better, but when used in our Motion Matching demo I'm not sure how much of an improvement they really are over the basic exponential decay:
I'm certain there are some more clever heuristics that could be used here, but I'm not sure exactly what they could be! If you have any interesting ideas I would love to hear them.
Rather than relying on heuristics, what about training a Neural Network to do this extrapolation for us? We can train a network to predict the next pose and velocity given the current pose and velocity and use this each frame to extrapolate.
More specifically, let's setup a network that predicts a velocity that takes us from the current pose to the next pose. Then, during training we can use this velocity prediction to integrate the pose forward in time, and feed the result back into the network until we have produced a small window of animation (let's say 30 frames). This motion we can compare to the ground truth, using a forward kinematics loss, and update the network weights. You can find the full training code here.
(Aside: notice how this network is similar to the Stepper in Learned Motion Matching - the only real difference being that we are working directly with the joints, rather than the motion matching features and learned additional features.)
After training, the extrapolated motion from the network looks something like this:
Wow, that looks pretty good! Admittedly this is testing on the training set, but I'm still impressed at how well it does. And testing on the training set is not wholly unrealistic in this case given that we can expect to be able to train this network on all of the animations we use in our animation system.
It is also interesting to note how small this network is. This network is only 300Kb of weights (which could likely be made half the size by quantizing to 16-bit), and yet it seems to have memorized effectively about 20 minutes of the motion data (albeit in a lossy way). I can imagine a setup using a network like this along with keyframes stored every N frames to effectively compress motion data.
Here is how it looks when used with Motion Matching:
The motion quality here is definitely an improvement over the heuristic methods, and we have no problem setting the blend time to something very large as our network can run for a long time without introducing bad posing.
Having to evaluate a Neural Network each frame to extrapolate is obviously more expensive than a simple heuristic method - but with a relatively small network (like the one in this example with 2 layers and 128 hidden units per layer) and my somewhat ad-hoc implementation on my laptop, it still takes only ~30us per frame. I am certain we could make this network even smaller since we only require a very approximate result for the extrapolation.
So that's dead-blending - a simple approach to inertialization that involves extrapolating the source animation and blending it into the destination where we can extrapolate the animation either with heuristics or data-driven approaches. You can find the full source code for the experiments shown in this article here. And I've added the dead blending setup to my springs environment too, which you can find here.
Appendix: If you're interested in some more tricks that can help with dead blending check out my follow up here about my implementation in Unreal Engine.